Gruebler's Equation for calculating Degrees of Freedom of the Mechanism

Mechanism with 1 degree of freedom

To design the mechanism, the first thing we should check is the number of degrees of freedom (DOF) of the mechanism. The degree of freedom is the number of inputs required to control the position of all links of the mechanism. It's usually the number of actuators needed to operate the mechanism. 

We can use Gruebler's equation to calculate the number of degrees of freedom of the mechanism as follows.

Gruebler's Equation

where:

F = number of degrees of freedom

n = total number of links in the mechanism

L = total number of lower pairs (1 DOF such as pins and sliding joints)

H = total number of higher pairs (2 DOF such as cam and gear joints)

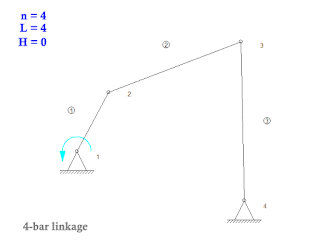4-bar linkage

In the machine, we often require one degree of freedom which we can position all linkages with only 1 actuator. The four-bar linkage as shown in the picture is the example of the mechanism with 1 DOF. It has 4 links (3 bars with 1 ground link) and 4 revolute joints which the degree of freedom (F) can be calculated as follows.

• n = 4 --- 4 links
• L = 4 --- 4 revoulte joints
• H = 0 --- no higher pairs
• F = 3(4-1) - 2(4) - 0 = 1

Another example of 1 DOF mechanism is the slider-crank mechanism where it has the following number of links and joints.

Slider-Crank Mechanism

• n = 4 --- 2 links + 1 ground link + 1 slider
• L = 4 --- 3 pins + 1 slider
• H = 0 --- no higher pairs
• F = 3(4-1) - 2(4) - 0 = 1

The gears mechanism also has 1 DOF since it has the following values.

Gears Mechanism

• n = 3 --- 2 gears + 1 ground link
• L = 2 --- 2 revolute joints
• H = 1 --- 1 gear joint
• F = 3(3-1) - 2(2) - 1 = 1

These 3 examples have 1 degree of freedom which requires only 1 actuator to move the mechanism. It could be a motor, an air cylinder, etc.

If we change the slider joint of the slider-crank mechanism to the fixed pin joint, the mechanism will be locked since it has 0 DOF which is considered as a structure. The calculation using Gruebler's equation is as follows.

Structure: Degree of freedom = 0

• n = 3 --- 2 links + 1 ground link
• L = 3 --- 3 pin joints
• H = 0 --- no cam or gear joints
• F = 3(3-1) - 2(3) - 0 = 0  --- F=0 then it can't move.

If one of the pin joint of the 4-bar linkage changes to the slider joint, it will increase both the number of links and number of lower pairs. This makes the mechanism unconstrained because it has 2 DOF and required 2 actuators to control the position of the mechanism.

• n = 5 --- 3 links + 1 slider + 1 ground link
• L = 5 --- 4 pin joints + 1 slider joint
• H = 0 --- no higher pairs
• F = 3(5-1) - 2(5) - 0 = 2 --- F > 1, the mechanism is unconstrained.

References:

• Machines & Mechanisms 3rd Edition, David H. Myszka
• 4 Basic Kinematics of Constrained Rigid Bodies
• Linkages sketch and animation using SAM 7.0 Mechanism Design Software