Grashof's Criterion: Crank-Rocker Four-Bar Mechanism

Grashof's criterion for Double Crank Four-Bar Mechanism is almost the same as Crank-Rocker Mechanism. They're both defined as S+L < P+Q. The difference is on the location of the shortest link (S). For double crank mechanism, S must be on the ground link (frame). But for the crank-rocker, S will be on the side link and it must be the input link.

We then move the shortest link from the frame to the side link on LH. With the help of SAM 7.0 Professional software (by Artas Engineering), it can display the paths of desired nodes as shown in the picture.

Grashof's Criterion: Crank-Rocker Mechanism using SAM 7.0 Professional Software

The pink curves represent paths of desired nodes. The input link which is now the shortest link is able to make a full revolution. It's called a crank. And the output (can be either L, P or Q) will only oscillate around its pivoting point. It's called a rocker. But if we change the driver to node 4 and let it drives from the link which is not the shortest link, it can't be reversed. The shortest link can't make a full revolution. What we have to do is to swap as shown in the following picture and it becomes a crank-rocker mechanism again which is now driving from the RH pivoting point.

Grashof's Criterion: Crank-Rocker Mechanism Driver on RH side

How can we see the velocity? From the path display, we can see how they move. But to see the velocity, we can choose to display the hodograph.

Path is the line that a moving point describes in the fixed reference system.

Velocity Hodograph is the locus of the arrowhead of the velocity vectors (rotated 90 degree) of a moving point. 

 The hodograph in SAM 7.0 is shown as follows.

Velocity Hodograph in SAM 7.0 The Ultimate Mechanism Designer

The lines on the outside of the path represent CCW direction of the node. And the lines at the inside of the path represent CW direction of the node. From the above picture, we can see that the input link of the crank-rocker mechanism rotates at a constant speed in CCW direction since the hodograph displays uniform lines at outside of the circular path. However, the output link oscillates back and forth with changes in velocity since there are lines of the hodograph both on the outside and inside of the its curve path. And we can quickly point out the position where the mechanism has highest velocity from longest line on the hodograph. SAM 7.0 is also able to plot various design parameters of the mechanism e.g. velocity, displacement, acceleration, length, etc. In the above picture, LH graph shows the velocity profile of the output link which can be traced manually. The following shows the hodograph of the double crank mechanism for a comparison.

Hodograph of Double Crank Mechanism

The following is the video showing how to use SAM 7.0 Software to simulate the double crank and crank-rocker mechanisms.

Grashof's Criterion: Four-bar Mechanism Double Crank

One of the most commonly used linkages is the four-bar linkage. It consists of 3 moving links and 1 ground link (also called a frame). There are 4 pin joints connected between those links. And from Gruebler's Equation, it's the mechanism with 1 degree of freedom (1DOF) which requires only 1 actuator to drive and control position of all linkages. The four-bar mechanism consists of the following components.

Four-bar mechanism components

The link that connects to the driver or power source is called the input link. The other link connected to the fixed pivot is called the output link. The remaining moving link connected between input and output links is called the coupler. It couples the motion of the input link to the output link.

There are different configurations of lengths of the four-bar mechanism and it results in different movements of the mechanism. Grashof's Criterion helps classifies into the following categories:

1. Double Crank --- also called a drag link mechanism
2. Crank-Rocker
3. Double Rocker
4. Change Point
5. Triple Rocker

In this post, we're going to explore the case of Double Crank which both input and output links are able to rotate through a full revolution. We use Autodesk ForceEffect app on Google chrome to illustrate and demonstrate how the mechanism moves. The links can be setup easily by just dragging. The exact length dimension can also be specified. Once we setup all required items i.e. links, pivots and drive, we can play and see the animation of the linkages with the path of desired tracing points.

Autodesk ForceEffect app on Google chrome

Grashof's criterion states that a four-bar mechanism has at least one revolving link if:

S + L ≤ P + Q

where:
S = length of the shortest link
L = length of the longest link
P = length of one of the intermediate length links
Q = length of the other intermediate length link

For the Double Crank category, the following criteria must be satisfied:

Double Crank:

• S + L < P + Q
• S is the length of the frame (ground link)

So we setup the links in ForceEffect app as follows.

Grashof's Criteria for Double Crank 4-bar Mechanism

The shortest link (S) is the frame which is 400 mm long. The length of the longest link (L) is 1300 mm. The remaining 2 intermediate links (P and Q) have length 700 mm and 1200 mm.

This satisfies Grashof's criteria since (S)400 + (L)1300 < (P)700 + (Q)1200. And this is how this mechanism moves.

Paths of double crank four-bar mechanism

Both input and output links can make a full revolution as desired. Let's find more details of other categories in later post.

The following video shows how to use ForceEffect app to simulate the motion of double crank four-bar linkage.

Reference:

• Machines & Mechanisms 3rd edition, David H. Myszka
• Autodesk ForceEffect

Gruebler's Equation for calculating Degrees of Freedom of the Mechanism

Mechanism with 1 degree of freedom

To design the mechanism, the first thing we should check is the number of degrees of freedom (DOF) of the mechanism. The degree of freedom is the number of inputs required to control the position of all links of the mechanism. It's usually the number of actuators needed to operate the mechanism. 

We can use Gruebler's equation to calculate the number of degrees of freedom of the mechanism as follows.

Gruebler's Equation

where:

F = number of degrees of freedom

n = total number of links in the mechanism

L = total number of lower pairs (1 DOF such as pins and sliding joints)

H = total number of higher pairs (2 DOF such as cam and gear joints)

4-bar linkage

In the machine, we often require one degree of freedom which we can position all linkages with only 1 actuator. The four-bar linkage as shown in the picture is the example of the mechanism with 1 DOF. It has 4 links (3 bars with 1 ground link) and 4 revolute joints which the degree of freedom (F) can be calculated as follows.

• n = 4 --- 4 links
• L = 4 --- 4 revoulte joints
• H = 0 --- no higher pairs
• F = 3(4-1) - 2(4) - 0 = 1

Another example of 1 DOF mechanism is the slider-crank mechanism where it has the following number of links and joints.

Slider-Crank Mechanism

• n = 4 --- 2 links + 1 ground link + 1 slider
• L = 4 --- 3 pins + 1 slider
• H = 0 --- no higher pairs
• F = 3(4-1) - 2(4) - 0 = 1

The gears mechanism also has 1 DOF since it has the following values.

Gears Mechanism

• n = 3 --- 2 gears + 1 ground link
• L = 2 --- 2 revolute joints
• H = 1 --- 1 gear joint
• F = 3(3-1) - 2(2) - 1 = 1

These 3 examples have 1 degree of freedom which requires only 1 actuator to move the mechanism. It could be a motor, an air cylinder, etc.

If we change the slider joint of the slider-crank mechanism to the fixed pin joint, the mechanism will be locked since it has 0 DOF which is considered as a structure. The calculation using Gruebler's equation is as follows.

Structure: Degree of freedom = 0

• n = 3 --- 2 links + 1 ground link
• L = 3 --- 3 pin joints
• H = 0 --- no cam or gear joints
• F = 3(3-1) - 2(3) - 0 = 0  --- F=0 then it can't move.

If one of the pin joint of the 4-bar linkage changes to the slider joint, it will increase both the number of links and number of lower pairs. This makes the mechanism unconstrained because it has 2 DOF and required 2 actuators to control the position of the mechanism.

• n = 5 --- 3 links + 1 slider + 1 ground link
• L = 5 --- 4 pin joints + 1 slider joint
• H = 0 --- no higher pairs
• F = 3(5-1) - 2(5) - 0 = 2 --- F > 1, the mechanism is unconstrained.

References:

• Machines & Mechanisms 3rd Edition, David H. Myszka
• 4 Basic Kinematics of Constrained Rigid Bodies
• Linkages sketch and animation using SAM 7.0 Mechanism Design Software

Stiffness of a lever with eccentric loading - Part 2

Let's continue from the previous post. We clearly see that the small post must be shortened because it the weakest point and creates torsional load to the lever arm. We're going to try redesigning with a bent lever arm so that the loading point stays in the middle of the center line of the arm.

Lever bending to eliminate torsion

The eccentric distance "r₂" is shorter than previous design (r₁). It's now the eccentric dimension with respect to the bent portion of the lever. Torsion still exists at end portion which has shorter length. This gives much less torsion compared with the earlier design. It also eliminate the torsion from the longer part of the lever since the loading point stays at the center line of the lever.

Two lever designs at the same loading point

From the overlay, we can see that the pull rod connecting point is still at the same location. The lever arm still connect to the same hub. But we can reduce the length of the small post which is the pin for the pull rod connection. The longer portion of the lever is now under bending only. Most torsion has been eliminated. It exists at the small portion as explained.

Finite element analysis - displacement of the lever with bent end

Shortening the small post and keeping the loading point on the center line of the lever can reduce displacement from 2.4 mm to 1.6 mm (33% reduction). Small twisting is present at the end but there is no twisting over the long portion of the lever.

von Mises stress of the bent lever

The von Mises stress reduces about 77%. This improvement can be used in most cases even when the lever shaft is short and the pull rod location is beyond the lever hub location and it's stiffer than the big lever with small post. The following picture is the example of bent levers on the machine.

Example of a bent lever on the machine

Stiffness of a lever with eccentric loading - Part 1

A lever is a mechanical part that has arms and a fixed pivot used to transmit torque. The cross section of the arm is usually a rectangular shape which makes it stiff against bending. However, its stiffness may become lower if the loading point is not on the right place. We're going to see the effect of torsion on the lever with the improvement idea.

The following picture is the components of a general cam and lever system. The lever has the hub in the middle. It's where bearings are placed inside and it's the fixed pivoting point on a lever shaft (not shown). There are 2 arms to the left and the right. They're both welded to the hub and rotate together. The right arm is connected to a cam follower that rolls over cam surface. When the cam rotates the lever will swing up and down since there will be spring forces pushing the cam follower to keep contact with the cam surface all the time. The left arm has another point to connect to other machine parts, which usually is a pull rod. It will rotate at the same angle (degrees) with the right arm, but the distance (mm) may be different depending on a lever ratio.

Components of cam & lever system

The pull rod connecting point on the left in this example is not good since it has a long distance from the arm and the arm will not only be subjected to bending but also torsion. The following is the lever in the machine.

Lever with eccentric pull rod connecting point

The eccentric distance "r" usually comes from space limitation on the lever shaft. There may be some other machine parts blocking the lever and it can't move any further. The hub stays at the same location and the lever is just straight from the hub. Because of this, there will be a gap between the lever and the pull rod. That's why the designer add that small connection post at the end.

Load from the pull rod

The small post will be subjected to bending and the lever arm will also subjected to bending as well as torsion. If the distance "r₁" is much less then it could improve the stiffness. Here is the finite element analysis result of this lever.

Finite element analysis - displacement of the lever under eccentric load

We can see from the finite element analysis result that the lever bends down due to the load and it also twists to the right because of the eccentric load. However, the small post that connects to the pull rod reduces the overall stiffness since it also bends down.

von Mises stress of the lever under torsional load

The highest von Mises stress is at the weakest point on the small post as shown in the picture.

To reduce the overall displacement, the overall stiffness will improve. We can change some designs to eliminate the torsion away from the lever arm and reduce the length of the post. Let's see how it's done in the next post.

Stiffness of a welded straight square tube

To modify or improve process of the existing machine in a production line may have some constraints regarding available spaces. There may be other moving objects or fixed parts which obstruct mounting of newly design parts. The part that comes later may be more complex since it has a limited space for mounting. The green support, design C from earlier post, is the example.

Part with other object occupied spaces

This is the side view of the above picture. The moving object occupies the space above the horizontal square tube and the design is in the L shape as shown below in order to avoid interference.

Side view of design C

This green support takes both loads in x and z directions. The load in z will try to bend the part and the load in x will try to twist the part. The dimension L is quite long from the center of the horizontal tube and the torque which is product of F_x and L will easily twist the horizontal tube. Since L is long, only a few twisting degrees of the tube will result in having larger displacement at the end (at the top flange where the loads applied).

Loads on welded part (design C)

If there is no obstruction above the horizontal tube, we can then change the design not to form the L shape in order to avoid twisting of the tube as shown below.

Straight tube design when space is available

The force in z is still trying to bend the straight tube up. However, the force in x will not try to twist the tube anymore. It's trying to bend the tube to the left instead. And with this design we can reduce the mass from 0.92 kg of design C to 0.71 kg which is about 23% reduction. And here is the finite element analysis result using the same fixations and loads.

Finite element analysis result: displacement of straight tube design

Not only mass reduction, but also the stiffness increases. The displacement reduces from 9.7 mm of design C to 6.98 mm which is about 28% reduction. This is because we eliminate the torque from the tube. But of course, this is when there is available spaces above the horizontal tube of design C.

We will apply this torque reduction design to other applications in later posts. Please stay tuned!

Stiffness comparison of welded parts - Part 4

As we can see from previous post that design C is still the best choice since it's light-weight and relatively rigid compared to other designs. Design E is the most stiff design but it's also the most heavy design. Let's continue with the remaining 2 designs with 4 ribs at the mounting base to see whether they're better than design C or not.

Finite Element Analysis result: Displacement of Design G

The weight of this design is in the same level as design D, but it's more rigid. When compared to design A, its weight is 123% and the displacement is 72.8%. Then we increase lengths of those 4 ribs in order to reduce the displacement. This is design H which its mass increases to 133% of design A. Here is the FEA result.

Finite Element Analysis result: Displacement of Design H

The displacement is 9.72 mm which is 65.8% of design A. It's comparable to design C, but heavier. So design C is still the best choice. It's simple, not difficult to make, light-weight and stiff. The following is the summary of displacement and mass of all designs. The value in percentages are compared to design A.

Summary of displacement and mass of different welding designs

 The red, yellow and green are used to express what is desirable and what isn't. Red is undesirable and green is desirable.

We hope the experiment about the stiffness using finite element analysis in these 4 posts may provide you the idea of improvement. Sometimes, we add extra materials (more weight, more cost) but gain very little. Sometimes, only minor changes change significantly improve the design with acceptable weight and cost.

The following is the video showing more details of this experiment.


Design C is good when we can't have any parts above the horizontal tube. It may interfere with other parts, for instance. However, if there is no space limitation above the horizontal tube, we could greatly improve the stiffness of the structure and reduce the weight. Let's find out in the next post.

Stiffness comparison of welded parts - Part 3

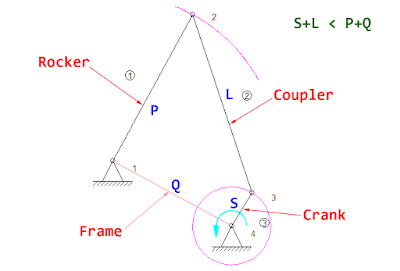
There are a lot of designs of welded parts which are commonly seen. The design A as shown in previous post are one of the examples. However, there are some more examples which may seem to be much better than design C. Let's have a look at these 5 more designs and see how stiff they are. Normally, to make the welded parts more rigid, we have to add some more materials. This usually increases the weight (mass) of the part which, in most cases, is undesirable. Therefore, we want to get the design that provides as low as possible displacement with relatively small increases of the weight. These are 5 new designs to consider.

Five more designs of welded parts for stiffness comparison

Let's recall the designs from previous post (design A, B and C) in order to compare with these new designs.

Welded parts of previous analysis

Design C is the best solution compared with design A and B as shown in earlier post. However, we may think that design A is not so bad, probably we can add 2 more plates on both sides of the square tubes which will be stronger for torsional load. Because of this, we get design D which we have more masses due to those 2 plates. The mass of design D is 1.12 kg which is 124% of the original mass (design A). What about the displacement?

Finite Element Analysis result: Displacement of Design D

The displacement of this design is in the same level as design A. Design A has displacement of 14.77 mm and this design has displacement of 14.49 mm. The bad thing is that it's heavier by 24% but still has the same displacement. We can see from the finite element analysis result that there is small displacement on the horizontal tube up to half of its length which is good. But larger displacement starts at the end of the tube. Length of the rib is not long enough to prevent the horizontal tube from twisting.

Then, we have a new improvement by making those 2 side ribs larger as shown in design E. We expect to see much reduction of displacement because the ribs are all over the length of the tube.

Here is the FEA result.

Finite Element Analysis result: Displacement of Design E

The displacement is much less as expected. It has only 8.17 mm which is only 55.3% of the original design. We can reduce the displacement almost by half since those ribs make it strong against torsional load. However, we have to sacrifice much more weight. Total mass becomes 202% of the original design. So it's rigid, but heavy. Probably, we can reduce some weights but still get good stiffness.

We then have Design F which both side ribs are cut to reduce weight from 1.82 kg to 1.44 kg (160% of original mass). It's still quite heavy, but let's see the displacement.

Finite Element Analysis result: Displacement of Design F

This design is still not good since it's heavier than design C and has more displacement than design C. So among these 3 new designs, design E is the most rigid design but it's too heavy.

Let's continue in the next post for the remaining 2 designs.

Stiffness comparison of welded parts - Part 2

From [Stiffness comparison of welded parts - Part 1], we have 3 different designs of supports subjected to the same loads which we're going to compare their stiffness. Let's start with the Finite Element Analysis (FEA) model of design A.

Finite element analysis (FEA) model of Design A

The mounting plate on the right is constrained so that there is no displacement in x, y and z directions. The flange on the left is subjected to face loads in x and z directions which means the support is under bending and torsion. After solving the equations, we get the post processor result as follows.

FEA result: Displacement of Design A -- typical welding connection

The max displacement magnitude is 14.77 mm and displacement in x, y, and z are as follows.

• Max displacement in x = -12.2 mm
• Max displacement in y = 4.4 mm
• Max displacement in z = -7.5 mm

The same conditions applied on design B and C. And these are the FEA results.

FEA result: Displacement of Design B -- additional square tube

The max displacement magnitude is 10.77 mm (27% decreased) and displacement in x, y, and z are as follows.

• Max displacement in x = -10.1 mm (17% decreased)
• Max displacement in y = 3.2 mm (27% decreased)
• Max displacement in z = -2.4 mm (68% decreased)

The displacement in z direction reduces 68% since the additional square tube helps support the bending. The third tube also helps reduce torsion which result in reduction of displacement in x direction by 17%.

FEA result: Displacement of Design C -- reinforced plate inserted between square tubes

The max displacement magnitude is 9.7 mm (34% decreased) and displacement in x, y, and z are as follows.

• Max displacement in x = -8 mm (34% decreased compared to design A)
• Max displacement in y = 3.1 mm (29% decreased compared to design A)
• Max displacement in z = -4.8 mm (36% decreased compared to design A)

The displacement in z direction reduces 36% which is less than design B. However, when subjected to torsion, the displacement in x direction is much less than design B. This design is only adding a small piece of steel plate.

Summary:

• Displacement Magnitude:
• Design A = 14.77 mm (100%)
• Design B = 10.77 mm (-27%)
• Design C = 9.7 mm (-34%)
• Mass:
• Design A = 0.9 kg (100%)
• Design B = 1.3 kg (+44%)
• Design C = 0.92 kg (+2%)

So design C could improve stiffness with small increment of mass and it isn't difficult to do. There may be other better designs compared to design C, but this is one of the improvements that we can easily gain by minor changes to design.

The following video shows the 3D model in Unigraphics and finite element analysis model with results in LISA finite element analysis software.

Stiffness comparison of welded parts - Part 1

In the machine, we usually make parts to support other machine components from standard steel profiles because they are relatively low cost. In this post, we're going to see how different constructions affect the stiffness of the welded parts. We have 3 different constructions of supports as shown in the picture.

Supports with different constructions

The constructions are slightly different.

• A -- typical welding (mass = 0.9 kg)
• B -- typical welding with extra tube (mass = 1.3 kg)
• C -- square tubes welding with thin plate insertion between tubes (mass = 0.92 kg)

All 3 constructions are subjected to the same forces and constraints as shown in the picture. Main parts are square tubes size 25 mm x 25 mm with thickness of 2 mm. The flange on the right is the mounting plate. It is constrained not to move in x, y and z directions. And we assume this is the only mounting plate allowed to use due to the space limitation in the machine.

Welded square tubes subjected to face loads

There is another flange on the left is subjected to face loads in both x and z directions. So we can expect the displacement of the parts to the left (-x direction) and up (+y direction) directions when loaded.

Let's start with design A -- typical welding with 45 deg angle connection. There is only small area on the perimeter for welding.

Design A: Cut-away picture of typical welded square tubes with 45 deg. connection

Design B is the extended version of design A. An additional square tube is welded to withstand more forces but we get more weight and required more space. Assume there is nothing above the L-shape welded part and we can put additional square tube as shown in the picture.

Design B: Typical welded square tubes with extra support

Design C is the modified version of design A where we insert a thin steel plate (thickness = 2 mm) between both square tubes.

Design C: Cut-away picture of welded parts with a reinforced steel plate

Let's see how we setup the finite element model with constraints and loads in the next post.

Moment of inertia

The Moment of Inertia or Mass Moment of Inertia is the measure of a body's resistance to change in it's rotational speed. The moment of inertia must be specified with respect to a chosen rotational axis.
The moment of inertia depends on the body's mass distribution and the rotational axis chosen. The larger moment of inertia requiring more torque to change the body's rotational speed.

A point mass
The moment of inertia is the mass times the radius from the rotational axis squared.

Moment of Inertia of Point Mass

A collection of point mass
The moment of inertia is just the sum of the point mass moment of inertia.

Moment of Inertia of Collection of Point Mass

A continuous mass distributions 
The moment of inertia require an infinite sum of all the point mass moment of inertia which make up the whole part. This can be calculated by an integration over the whole mass.

Moment of Inertia of Continuous Mass Distributions

A common shape
For a common shape, we usually calculate the moment of inertia about the certain point and use it to apply for another rotation axis by use the parallel axis theorem.

Moment of Inertia of Common Shape Body

Parallel Axis Theorem
The moment of inertia about any rotation axis which parallel to a certain axis at center of mass (I_parallel)  is the moment of inertia about the center of mass (I_cm) plus the product of mass times the distance between the center of mass and the rotation axis squared.

Parallel Axis Theorem

Parallel Axis Theorem can also apply to any rotation axis which parallel to  any certain axis at a point that already know the standard moment of inertia (I_xx , I_yy or I_zz).

Parallel Axis Theorem & Radius of Gyration

Radius of gyration [K]
It is the distance from a rotation axis to a certain point which the mass of a body may be assumed to be concentrated and at which the moment of inertia will be equal to the moment of inertia of the actual mass about the rotation axis.